軌跡#2
除外点
除外点
小・中学校で三角形や長方形の上を動き回って散々受験生を苦しめた 点 $ \mathrm P$、今度は $ xy $ 平面上を自由自在に動いて高校生を苦しめる。
はじめに
誰しも一度は「計算で答えは出るけど何が起こっているかわからない」という気持ち悪い感覚を味わったことがあるでしょう。特に軌跡は「逆チェック」「除外点」という厄介な存在があり、計算の方ではたとえば 「 $ \mathrm P(x,y), \quad \mathrm Q(s,t) $ とおいて $ \mathrm Q $ の座標を $ x,y $ で表し、 $ \mathrm Q $ の関係式に代入することで $ s,t $ を消去する」 のようなちょっと軌跡特有の解き方(!?)があって、とりあえず「軌跡は計算でゴリ押せばいい、逆チェックの言葉は減点されないためのおまじない」と思ってしまうのも無理はありません。
第1話ではまず「図形と方程式」の復習をします。方程式の意味が不安な人は特に読んでください。次に簡単な例題を通して「逆チェック」の意味について解説します。（あまりくどくは書かないので安心してください。）
第2話では媒介変数表示された点の軌跡について扱います。もう「 $ t $ を消去して…」なんて言いません。
嘘です。第2話では除外点について説明しています。
図形と方程式
「図形と方程式」では、文字通り方程式が表している図形を扱います。ではその「方程式が表している図形」とは一体なんでしょうか？
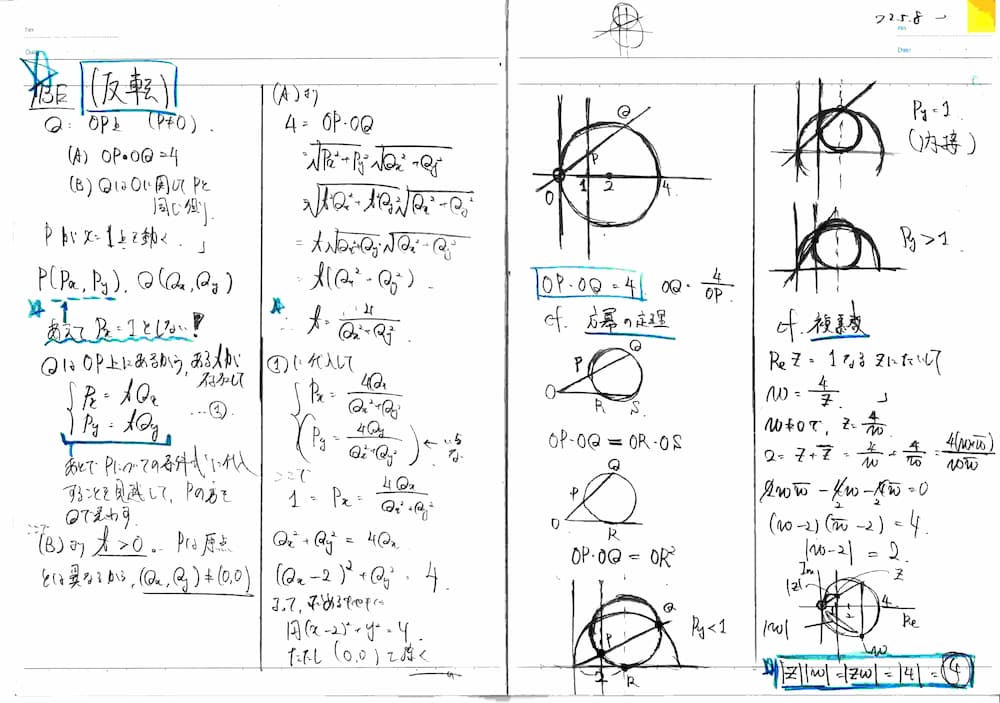
「直線 $ \boldsymbol{y=x} $」 という言葉を見たら、すぐに次のようなグラフが頭に浮かぶと思います。
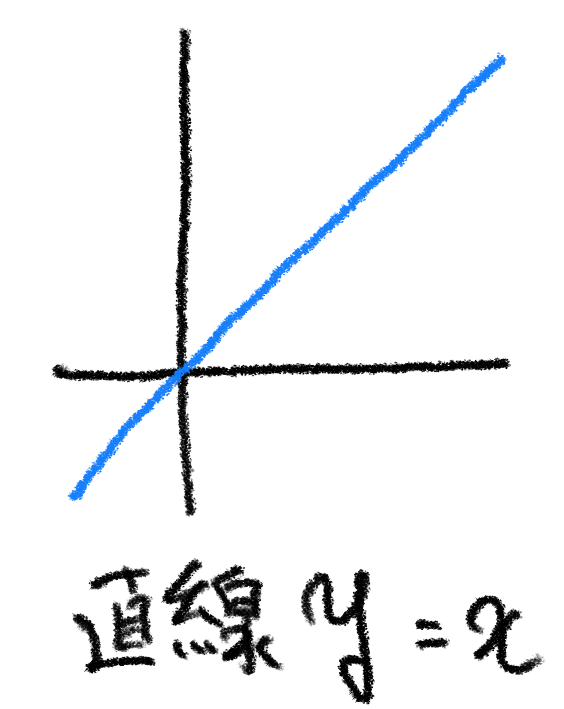
直線であることをいったん忘れて、「 $ y=x $ 」という式を平面上の点の条件式としてみるとどうでしょうか。
この式は「その点の $ \boldsymbol y $ 座標の値が $ \boldsymbol x $ 座標の値に等しい」という条件を表しているように見えませんか？
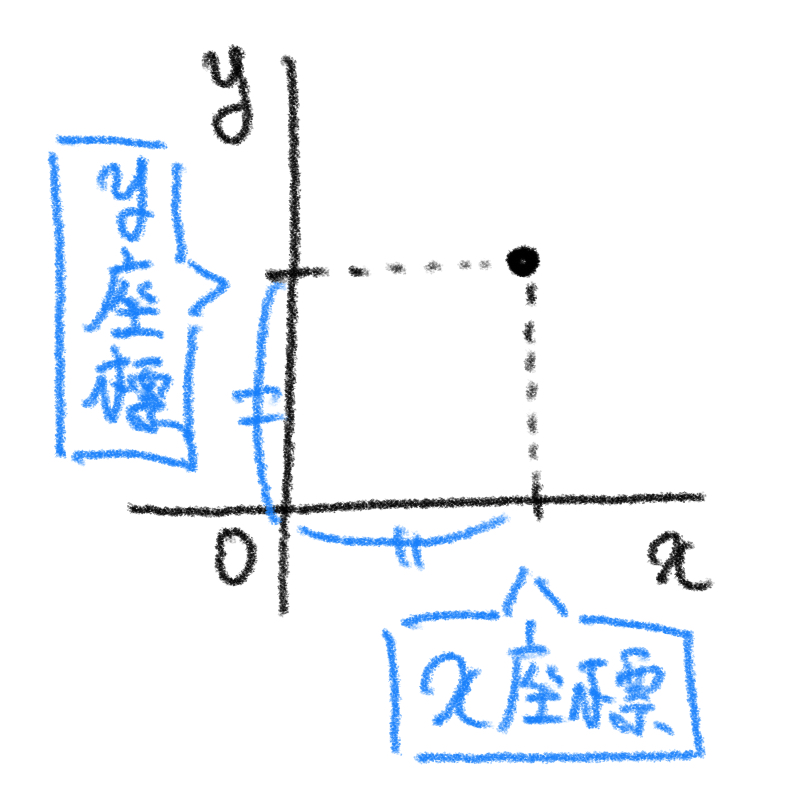
例えば点 $ (1,1) $ は $ y $ 座標の値も $ x $ 座標の値も $ 1 $ で等しいので方程式を満たします。
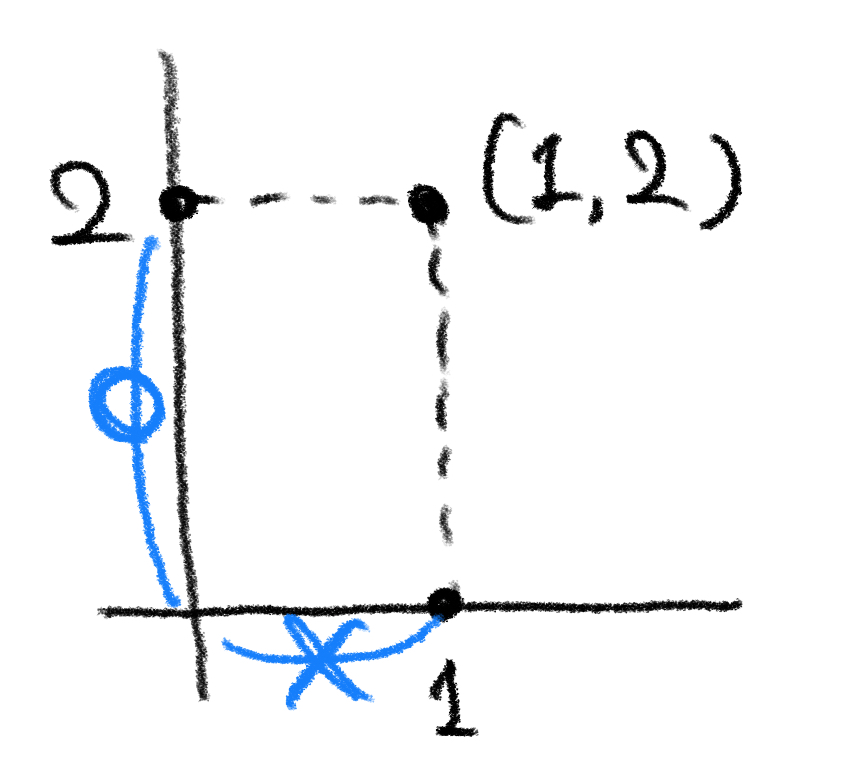
$ x $ 座標と $ y $ 座標の値が等しい点は $ (1,1) $ 以外にもあります。
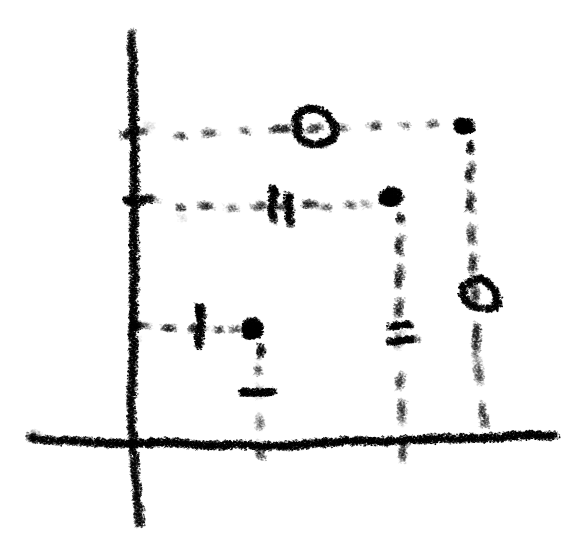
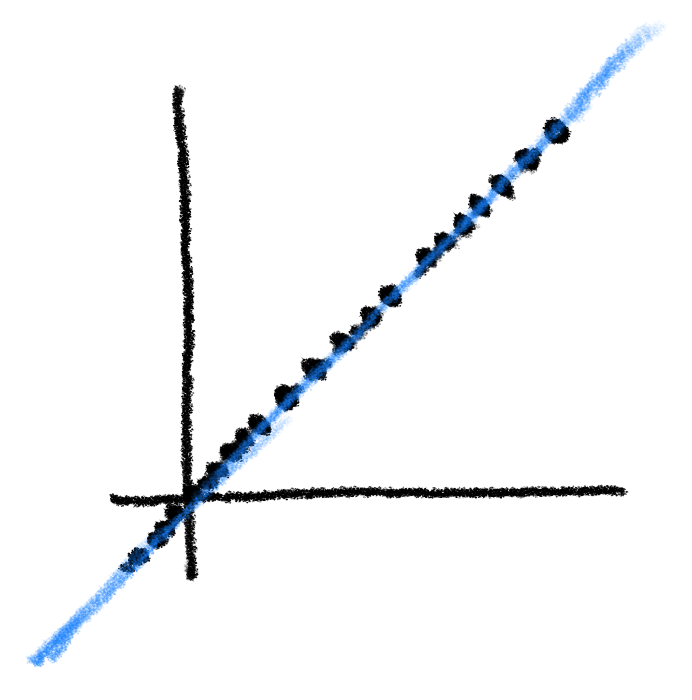
隙間なく埋め尽くしているのですから、逆に直線 $\boldsymbol{y=x} $ 上のどこの点を取っても必ず $ \boldsymbol x $ 座標と $ \boldsymbol y $ 座標が等しくなっています。
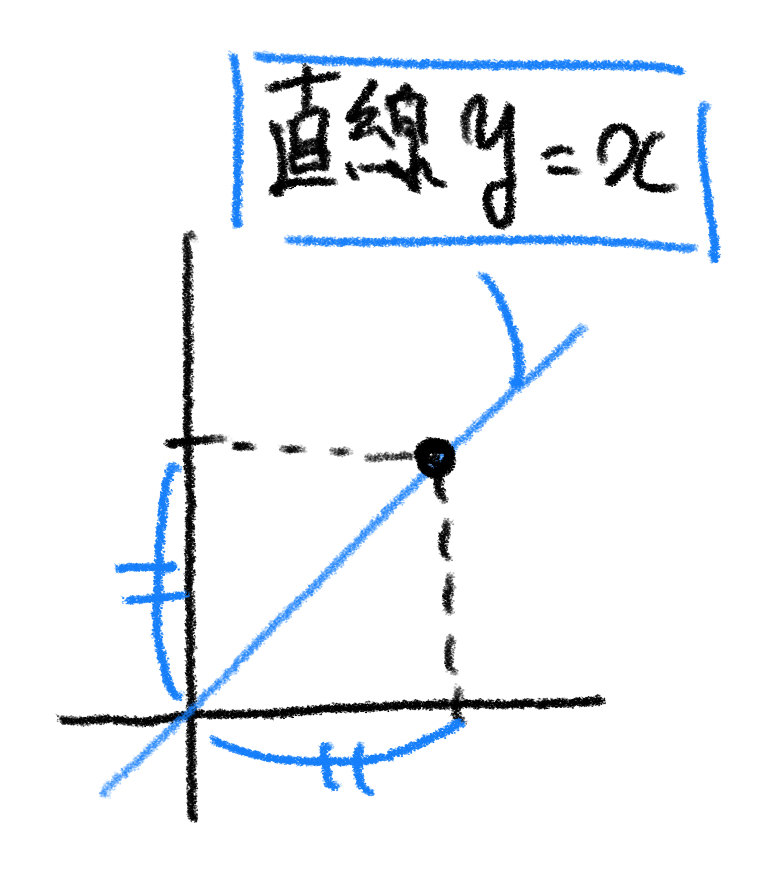
条件 $ y=x $ をみたすような点を全て集めたら直線になりました。そこで、この直線自体を「直線 $ \boldsymbol{y=x} $ 」という名前で呼んでしまおうというのが図形の方程式の発想です。
つまり、「直線 $ y=x $ 」や「円 $ x^2+y^2=1 $ 」などの $ x,y $ についての方程式で表されたは、方程式をみたすような点を全て集めたもののことなのです。[2]
方程式で表された図形は、方程式をみたす点の集まりだ！
軌跡を求める手順
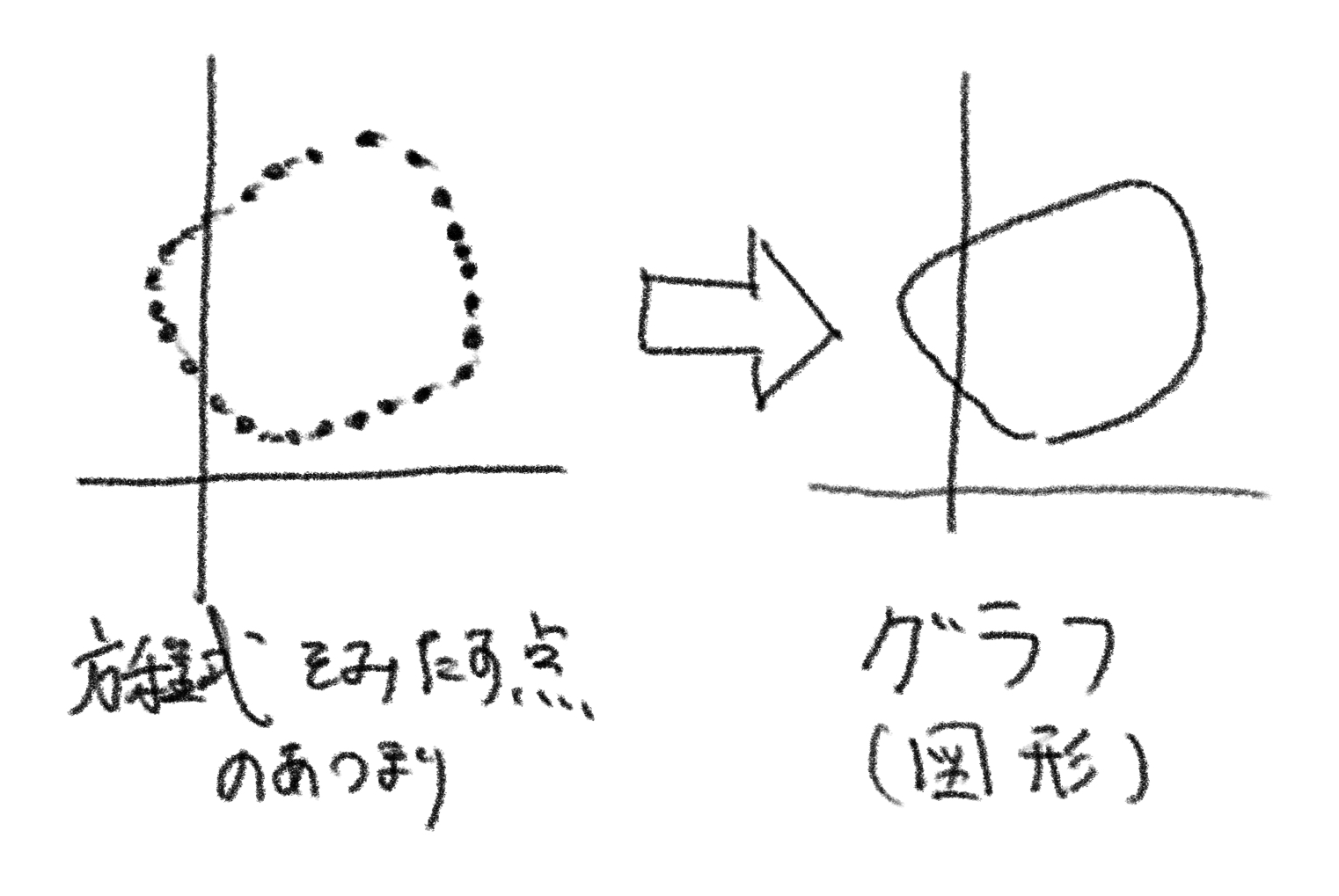
以上のことを踏まえて、本題の軌跡に入りましょう。
とりあえずは深く考えなくていいので、次の軌跡を求める手順をみてください。
軌跡を求める手順
与えられた条件をみたす点 $\mathrm P $ の軌跡は次のように求められる。
言葉にすると長いですから、例題を通してひとつづつ見ていきましょう。
例題
2点 $ \mathrm A(0,1),\; \mathrm B(1,0) $ からの距離が等しい点Pの座標を求めよ。
解答例
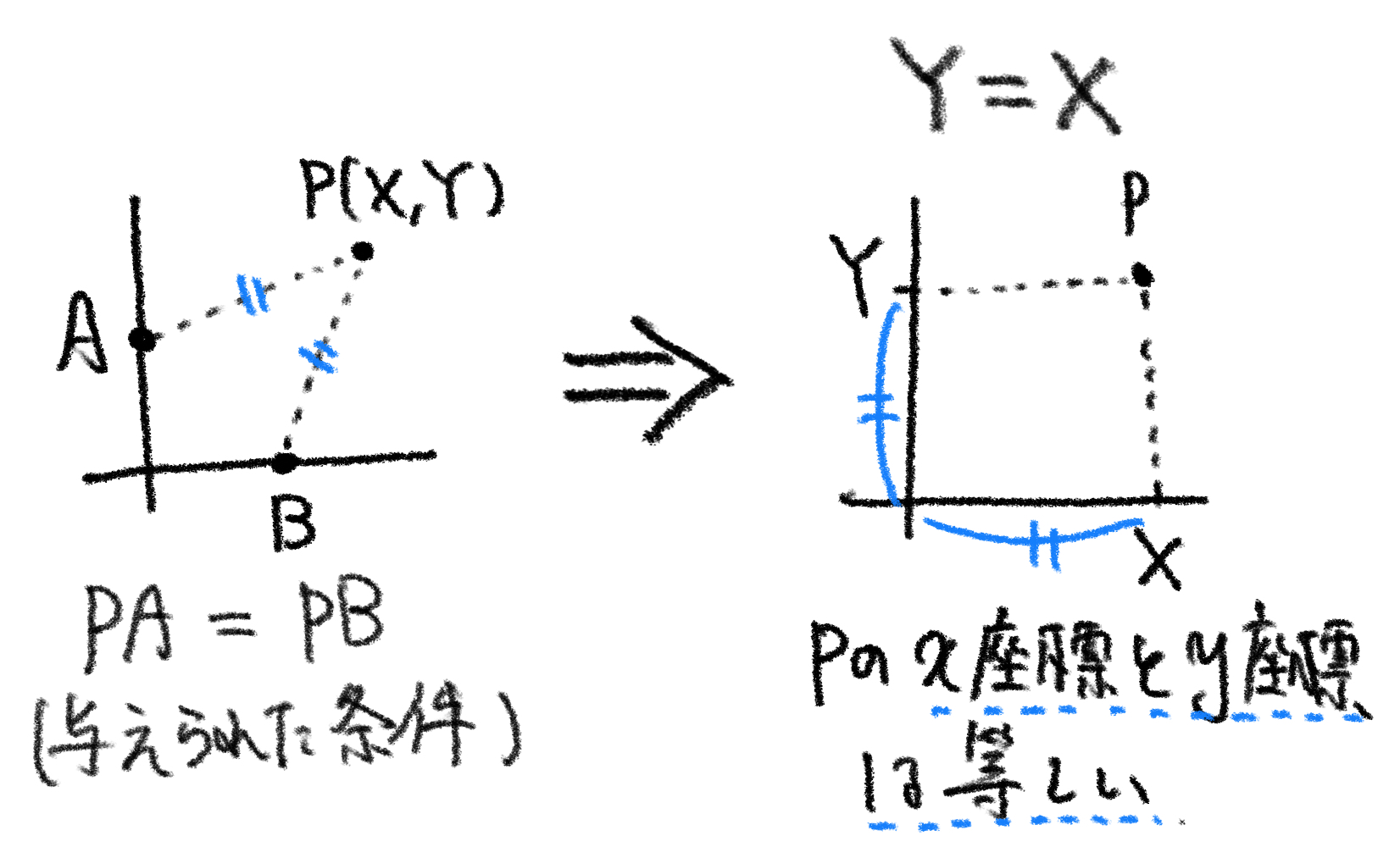
点 $\mathrm P $ の座標を $\mathrm P(X,Y) $ とすると（ …① ）、 三平方の定理より $$ \mathrm{AP}^2=X^2+(Y-1)^2 $$ $$ \mathrm{BP}^2=(X-1)^2+Y^2 $$
$ \mathrm{AP}=\mathrm{BP} $ より $ \mathrm{AP}^2=\mathrm{BP}^2 $ であるから \begin{align} X^2+(Y-1)^2 &= (X-1)^2+Y^2 \\ -2Y &= -2X \\ Y &= X \end{align}
（ …② ）
したがって、点 $ \mathrm P $ は直線 $ y=x $ 上にある（…③）。
逆に、点 $ \mathrm P $ が直線 $ y=x $ 上にあるとき条件を満たすことかどうか調べる。
点 $ \mathrm P $ が直線 $ y=x $ 上にあるとき、その座標は $$ \mathrm P(t,t) \quad\left(t\text{は実数}\right)$$ と表せる。
三平方の定理より $$ \mathrm{AP}=\sqrt{t^2+(t-1)^2} $$ $$ \mathrm{BP}=\sqrt{(t-1)^2+t^2} $$ であるから $$ \mathrm{AP} = \mathrm{BP} $$
よって点 $ \mathrm{P} $ は（ $ \mathrm{A} $ および $ \mathrm{B} $ からの距離が等しいという）条件を満たす（…④）。
以上より、求める軌跡は
直線 $ \boldsymbol{y=x} $
1. 点 $ \mathrm P $ の座標を $ (X,Y) $ とおく
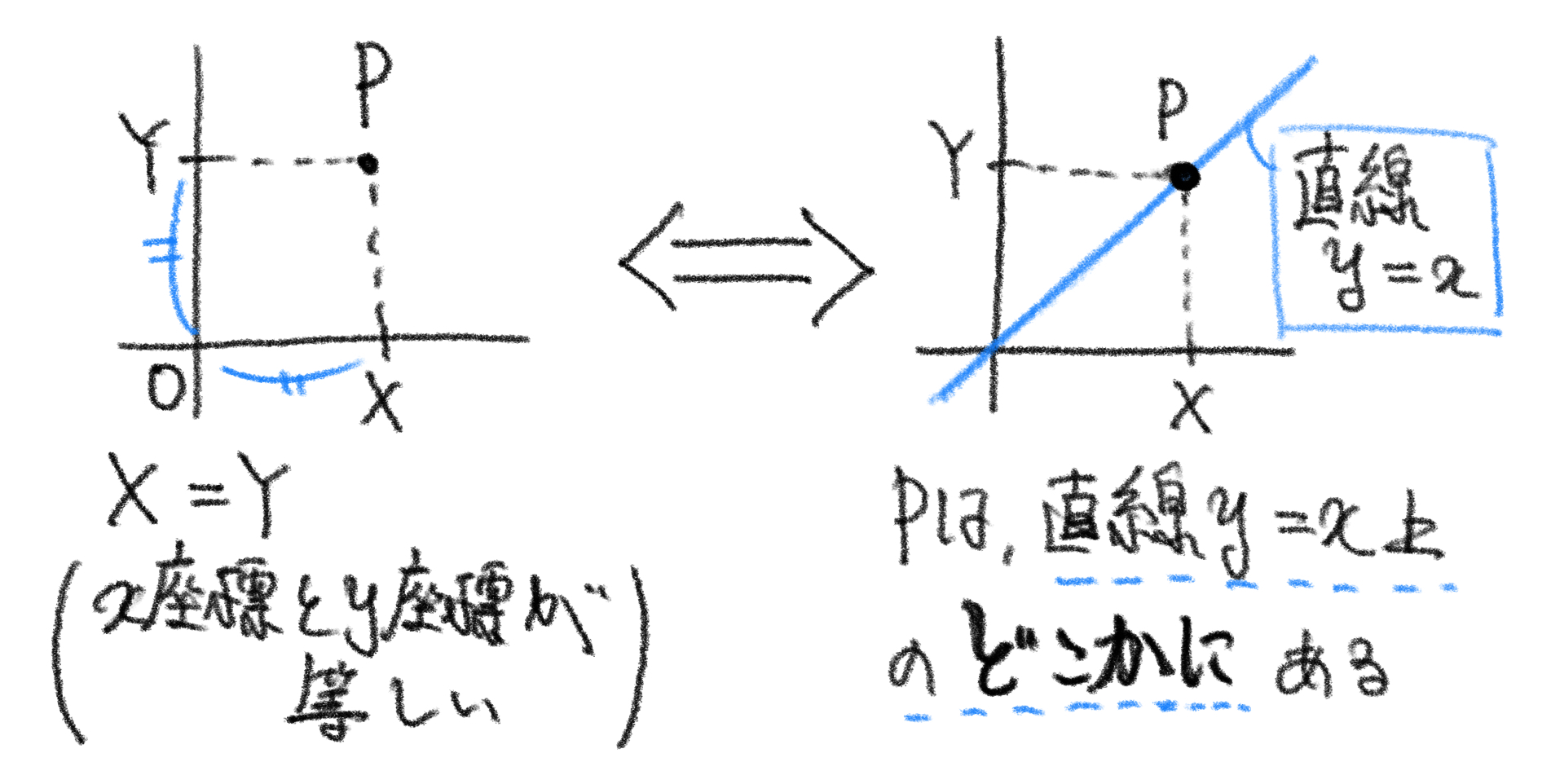
書いてあるとおり $ \mathrm P(X,Y) $ とおくだけなのですが、ここでひとつ注意してほしいことがあります。よく教科書なんかではこれを $ \mathrm P(x,y) $ のように小文字でおいていませんか？
これはだめではないのですが、あまりよろしくないです。それは実際に点 $ \mathrm P $ を座標平面上に書いてみるとわかります。
これは座標平面です。
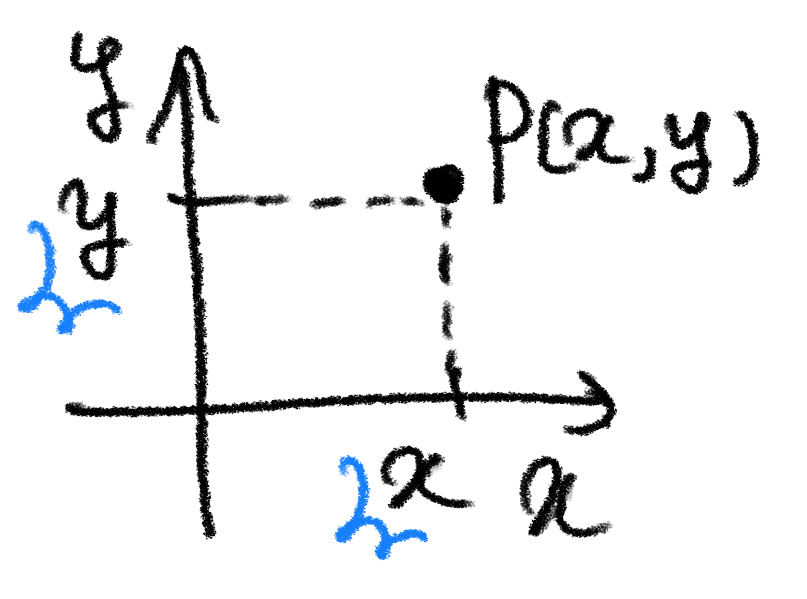
そこでこのような無用な混乱を避けるためにも、点の座標は $ (X,Y) $ とおくことにします。
ここではあまり立ち止まらず、「 $ (x,y) $ でおくと紛らわしいから $ (X,Y) $ で置くんだな〜」程度に思っていただいて大丈夫です。こう置くことの意味・メリットはあとでわかります。
2.与えられた条件から $\boldsymbol{X,Y} $ の関係式を導く
与えられた条件を式で表します。
点 $ \mathrm{P} $ が 点 $ \mathrm A(0,1) $ および $ \mathrm B(1,0) $ から等距離であるということは
$$ \mathrm{AP}=\mathrm{BP} $$
と書けます。このあとで三平方の定理を使うことを見越して両辺を2乗しておくと
$$ \mathrm{AP}^2=\mathrm{BP}^2 $$
が言えます。
ここで3点の座標は $ \mathrm A(0,1),\; \mathrm B(1,0),\; \mathrm{P}(X,Y) $ となっていますから、三平方の定理を用いればこの関係式を $ X,Y $ で表せます。
条件式を整理すると、 $ Y=X $ を得ます。
3.関係式をみたすような点の集まりがどんな図形になるか考える
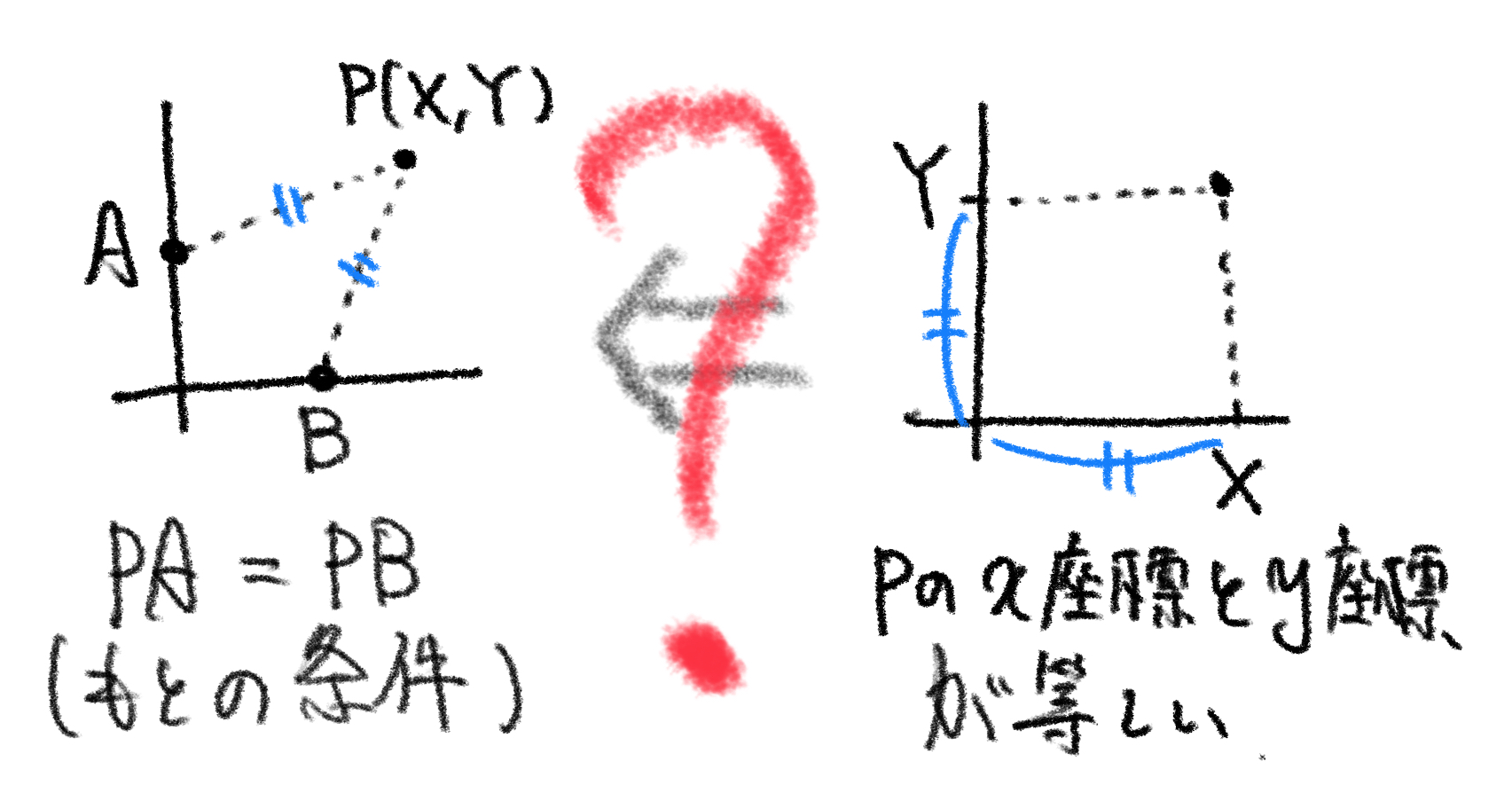
さて、このようにして関係式 $ Y=X $ が得られましたが、ここでそのまま「求める軌跡は直線 $ \boldsymbol{y=x} $ 」とすることはできません。なぜでしょうか。
関係式 $ Y=X $ は、点 $ \boldsymbol{\mathrm{P}} $ の座標についての条件です。
この式から読み取れるのは、条件（2点 $ \mathrm{A,B} $ からの距離が等しい）をみたす点 $ \mathrm{P} $ について、その $ \boldsymbol x $ 座標と $ \boldsymbol y $ 座標が等しいということだけです。
逆に、$\boldsymbol x $ 座標と $\boldsymbol y $ 座標の値が等しいような点がすべて条件（ $\boldsymbol{\mathrm{AP}=\mathrm{BP}} $ ）をみたしているかどうかは全くわからないのです。
「？？」と思った場合は こちら
そこで、4.のようにしてチェックする必要があります。
ともかく、点 $ \mathrm{P} $ の $ x $ 座標と $ y $ 座標が等しいことはわかりました。「図形と方程式」でみたように、このような点の集まりは直線 $ y=x $ ですから、点 $ \mathrm{P} $ が直線 $ y=x $ 上のどこかにあるということは間違いありません。
4.逆チェック
そこで逆チェックを行います。
$ \mathrm{P} $ が直線 $ y=x $ 上にある、すなわち $ \mathrm{P} $ の $ x $ 座標と $ y $ 座標が等しいときに、はじめの条件 $ \mathrm{AP}=\mathrm{BP} $ を満たすかどうか調べます。
$ x $ 座標と $ y $ 座標が等しいので、実数 $ t $ を用いて $ \mathrm{P}(t,t) $ と表すことができす。
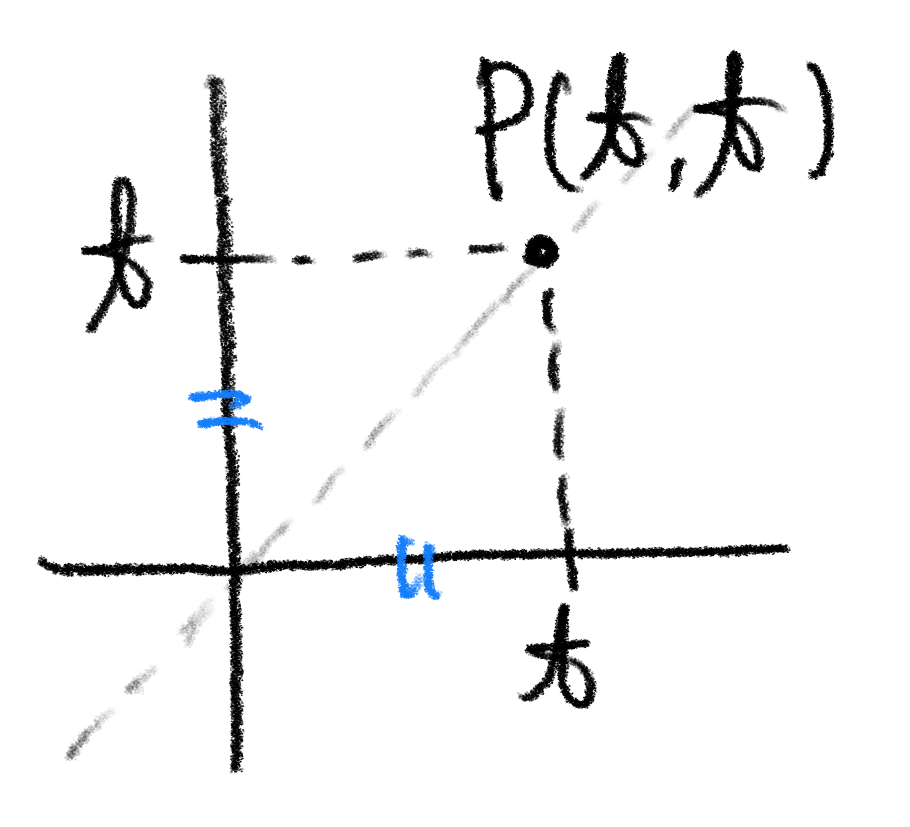
ここで晴れて逆、つまり $ \mathrm{P} $ の $ x $ 座標と $ y $ 座標が等しいときに、条件 $ \mathrm{AP}=\mathrm{BP} $ を満たすことが確かめられました。
5.求める軌跡
以上の議論から、ようやく求める軌跡は「直線 $ y=x $ 」であると答えることができます。
ここまでの流れを振り返ってみましょう。
- 点 $\mathrm P $ の座標を $ (X,Y) $ とおいた
- 与えられた条件 $ \mathrm{AP}=\mathrm{BP} $ から $ X,Y $ の関係式（ $ Y=X $ ）を導いた
- $ \mathrm{P} $ が直線 $ y=x $ 上にあることはわかった。逆が成り立つかどうかはまだわからない
- $ \mathrm{P}(t,t) $ とおいて $ \mathrm{AP} $ および $ \mathrm{BP} $ を計算することで、逆が成り立つことを確認した
- 求める軌跡は、直線 $ y=x $
4.の $ \mathrm{P}(t,t) $ とおく逆チェックは見慣れないかもしれませんね。通常はこの手順を省いて
逆に $ \boldsymbol{\mathrm{P}} $ が直線 $ \boldsymbol{y=x} $ 上にあるとき、条件を満たす
のように書いてしまいます。これは高校生だけに許された特権的なズルというべきもので、いちいち「$ \mathrm{P}(t,t) $ とおいて〜」などと書かずとも、この1行さえ書いてしまえば逆チェックを行ったとみなされます。
なぜ、ここまでしつこく逆チェックについて説明したのか。それは、この次の記事で扱う「除外点」をみるとわかります。
次の記事
質問・感想
注釈
[必要条件と十分条件]
命題「 $ p \Longrightarrow q $ 」が真だからといって、その逆「 $ q \Longrightarrow p $ 」が真であるとは限らない。たとえば $$ (x=2) \Longrightarrow (x^2=4) $$ は明らかに正しいが、その逆 $$ (x=2) \Longleftarrow (x^2=4) $$ は成り立たない。じっさい、 $ x=-2 $ のときも $ x^2=4 $ が成り立つから、 $ x^2=4 $ のとき必ずしも $ x=2 $ とはならない。
[1]
厳密な話をしだすとキリがないので割愛。
[2]
「図形と方程式」を習う前に扱っていたグラフは、 $ y=ax+b $（1次関数） や $ y=ax^2+bx+c $ （2次関数）、 $ y=\sin x $ など、yがxの関数となっているもの（$ y=f(x) $）だけだった。
ところが、「図形と方程式」で新たに習った円の方程式「 $ x^2+y^2=1 $ 」はyがxの関数になっていない。これはグラフを見れば明らかだ
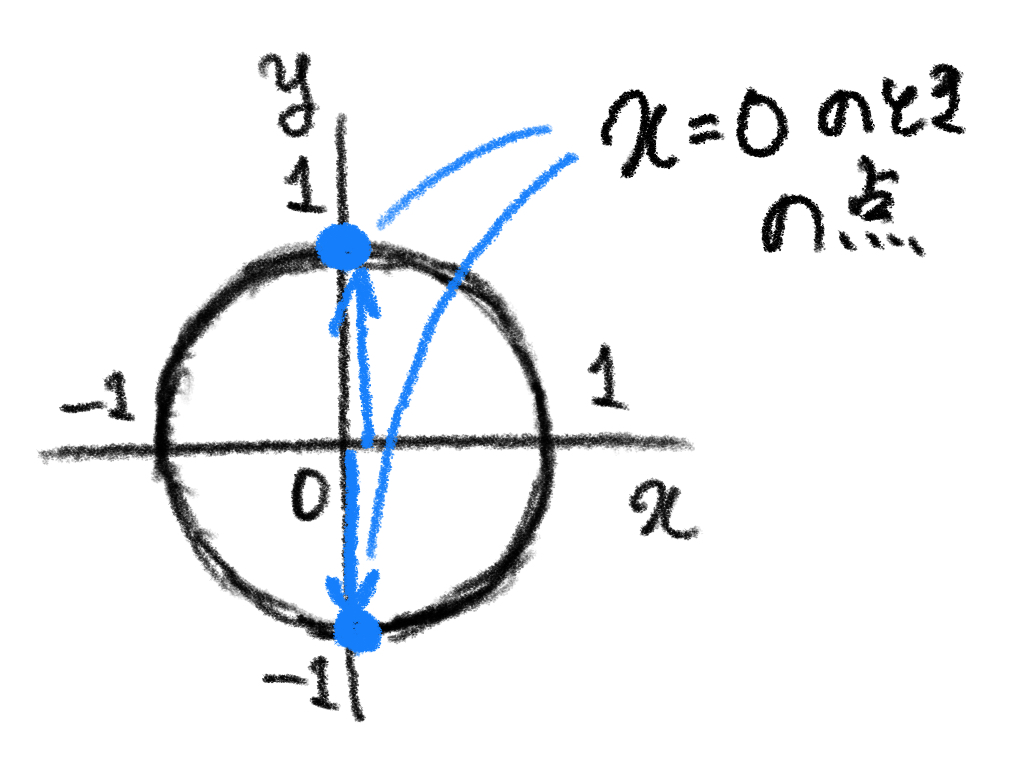
$ y $ が $ x $ の関数になっていないものも扱うから、一般にはこういう方程式を「 $ y=f(x) $ 」という形で表すことができない。そこで、次のような書き方をすることがある： 方程式 $ \boldsymbol{F(x,\;y)=0} $
$ F(x,\;y) $ という見慣れない形が出てきたが、これは $ x,y $ を含んだなんらかの式と思って差し支えない。たとえば $ x^3+x^2+y^2-y+xy+1 $ のようなものである。
この形を使えば、直線 $ y=ax+b $ は、 $ F(x,y)=ax-y+b $ として $$ ax-y+b=0 $$ のように、円 $ x^2+y^2=1 $ は、 $ F(x,y)=x^2+y^2-1 $ として $$ x^2+y^2-1=0 $$ のように表せる。
なお、2変数関数を知っていると、この $ F(x,\;y)=0 $ が表しているのが、関数 $ z=F(x,y) $ のグラフ（立体である！）を平面 $ z=0 $ で切ったときの切り口であることがわかる。