軌跡 #2 除外点 〜"逆チェック"の意味・②〜

前回の記事で「逆チェック」の意味については説明しましたが、いまいちピンと来ず、「結局『逆に〜』だけ書いておけばいいんでしょ？」と思っている方も多いと思います。そこで今回は「除外点」が発生し、常には逆が成り立たない例を紹介します。

三角形

例題

2点 $ \mathrm{A}(-4,0),\; \mathrm{B}(2,0) $ と点 $ \mathrm{P} $ を頂点とする 三角形 $ \mathrm{PAB} $ が $$ \mathrm{AP}:\mathrm{PB}=2:1 $$ をみたしている。
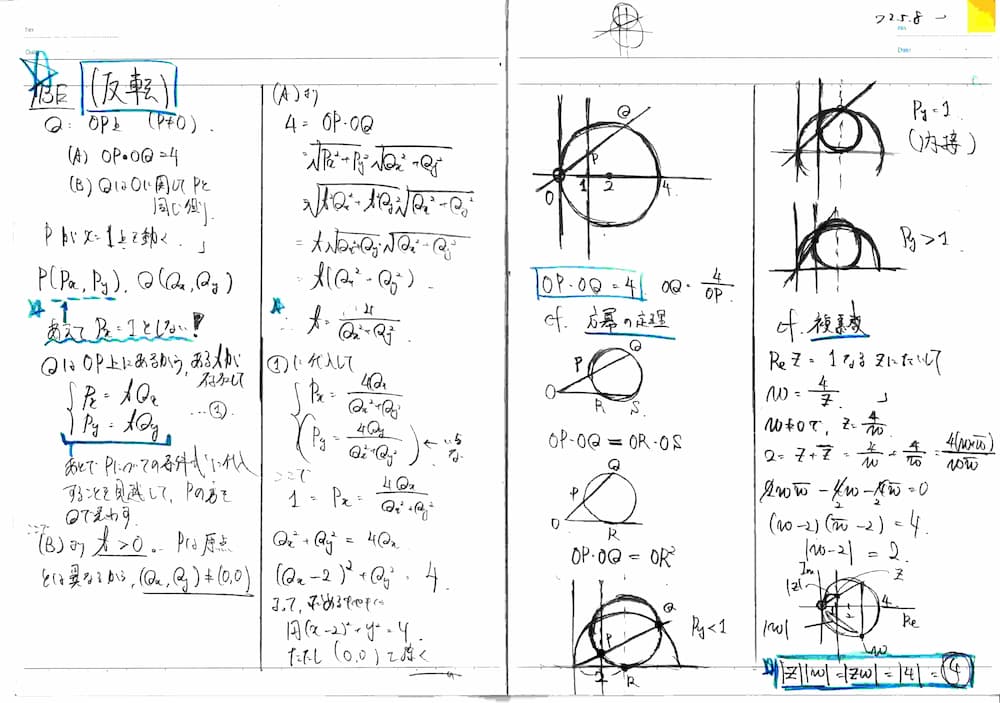
点 $ \mathrm{P} $ が動くときの軌跡を求めよ。

解答例

点 $ \mathrm{P} $ の座標を $ (X,Y) $ とすると、 $$ \mathrm{AP}^2=(X+4)^2+Y^2 $$ $$ \mathrm{BP}^2=(X-2)^2+Y^2 $$

$ \mathrm{AP}:\mathrm{BP}=2:1 $ すなわち $ \mathrm{AP}=2\mathrm{BP} $ より $ \mathrm{AP}^2=4\mathrm{BP}^2 $ であるから、 $$ (X+4)^2+Y^2 = 4\left\{(X-2)^2+Y^2\right\} $$ これを整理して \begin{align} 3X^2-24X+3Y^2&=0 \\ X^2-8X+Y^2&=0 \\ (X-4)^2+Y^2&=16 \end{align}

（…②）

したがって、点Pは円 $ (x-4)^2+y^2=16 $ 上にある（…③）。

---

逆に点Pがこの円の上にあるとする。

• $ \mathrm{P}(0,0) $ および $ \mathrm{P}(8,0) $ のとき、点Pは直線AB上にあるから三角形PABが成立しない
• そうでないとき条件を満たす。

（…④）

よって、求める軌跡は

円 $\boldsymbol{(x-4)^2+y^2=16} $
ただし点 $ \boldsymbol{(0,0)} $ および $ \boldsymbol{(8,0)} $ を除く

（…⑤　答）

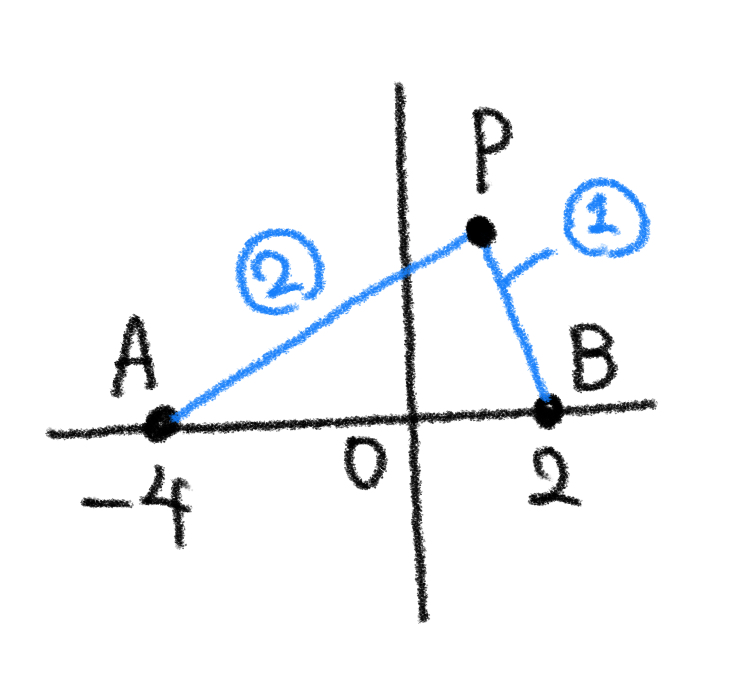
前回と同じようにして、②のように $ \boldsymbol{X,Y} $の関係式を導きます。今回は前回ほどシンプルにはならず、 $$ (X-4)^2+Y^2=16 $$ という式が得られました。

これをみた瞬間に「あ、円だ」と気づくわけですが、答えを出すにはまだ早すぎます。「円だ」と書きましたが、この時点でわかっているのは

ここで円 $ (x-4)^2+y^2=16 $ というのは、中心 $ (4,0) $, 半径 $ 4 $ の円のことを表す方程式です（図の青線）。

ですが、前にも述べたように逆にこの円周上の点がすべて条件を満たすかどうかはわかりません。ここで「とりあえず『逆に』って書いておけばいいんでしょ」って思っていると足元をすくわれます。

三角形ABP!!!!

最初の条件に「三角形ABPが〜」と書いてありました。ということは当然三角形ABPが存在していないといけません。三角形ABPは常に成立するでしょうか。

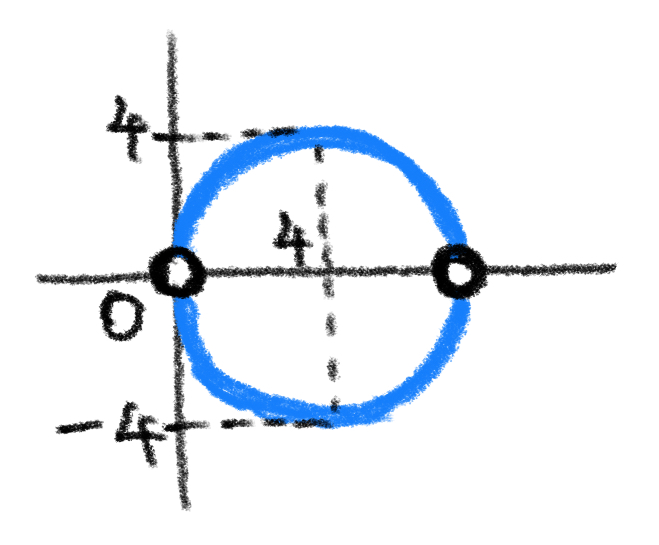
先ほどの「中心 $ (4,0) $, 半径 $ 4 $ の円」を、2点A,Bといっしょに図示するとこのようになります。

これをみれば、三角形ABPが成り立たない点があることは明らかです。

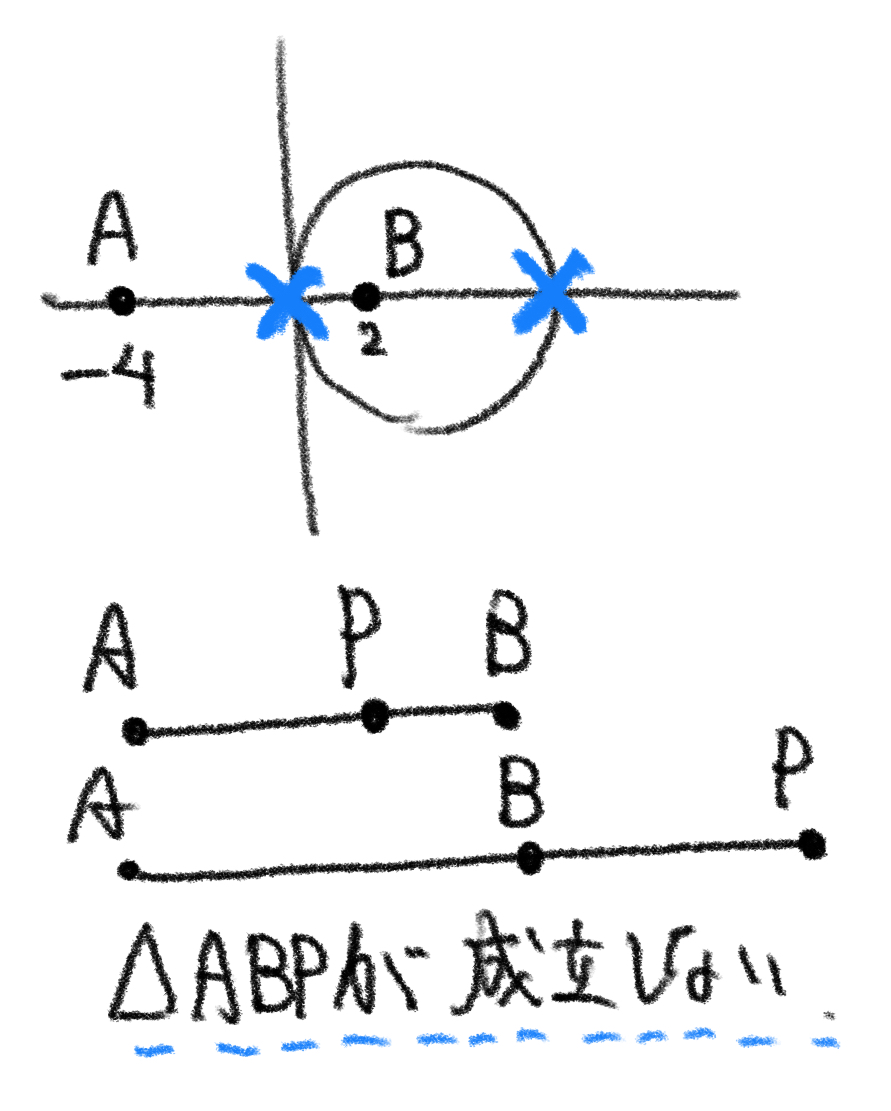
このことを逆チェックの記述に含めてあげる必要があります。

大抵の模範解答ではこのあとすぐ「よって、求める軌跡は〜」と答えてしまいますが、そういう「模範」解答を見ると、「え、この場合は逆チェックしなくていいの？　逆チェックするときとしないときの違いは何？？？？」という混乱に陥ってしまいます。

結論からいうと、「逆に〜」の記述は、意味を理解した上で、毎回必ず書くべきです。[1]

そこで今回も、

したがって、最終的な答えは

どんな時に除外点が発生するか

除外点が発生するようなケースは非常に限られていて、今回のように

後者に関しては、青チャートIIの重要例題111等を参照してください。

おわりに

いかがだったでしょうか。テスト前でバタバタしてしまって結局直前になってしまい申し訳ないです。モヤモヤしやすいこの単元の意味が少しでも伝わったら幸いです。質問等はお気軽にどうぞ

質問・感想