脱・場合わけ！ 絶対値つき不等式の領域 〜対称性利用〜

── 場合わけなんかしてたら時間足りねえよ

グラフの対称性

数式で書くとわかりづらいが、例えば方程式の中の文字 $\boldsymbol x $ を全て $\boldsymbol{-x} $ に置き換えても同じ方程式が得られるならば、そのグラフは $\boldsymbol y $ 軸対称であるということだ。例を見てみよう

例1

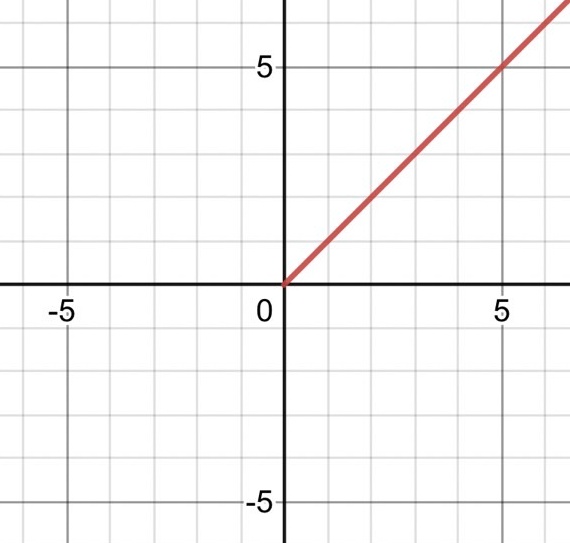
$ y=|x| $ のグラフを考える。
$ x $ を $ -x $ に置き換えると、左辺は変わらず、右辺も $$ |-x|=|x| $$ となって元の方程式と同じであるから、グラフは $ y $ 軸対称。 [1]

対称性より $ x\geqq 0 $ とすると、 $ y=x $。

対称性を戻して、

一工夫いる場合

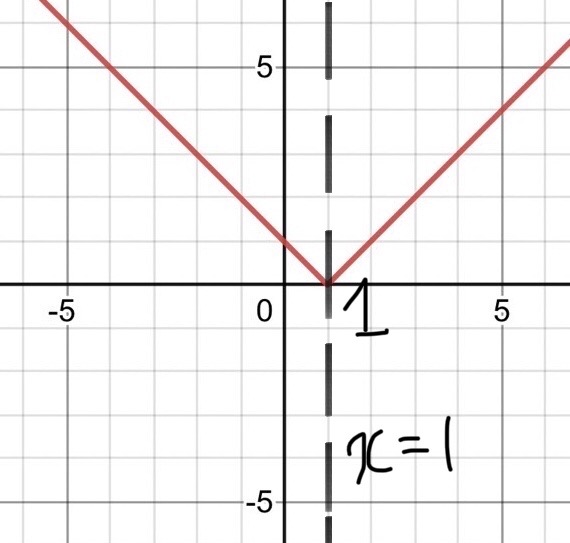
単純に $ x $ を $ -x $ に置き換えてみても、こんどは右辺が $$ |-x-1|=|x+1| $$ となってしまい、元の式 $ y=|x-1| $ に一致しない。対称性は使えないのだろうか。

諦めるのはまだ早い。先に答えをお見せしよう。

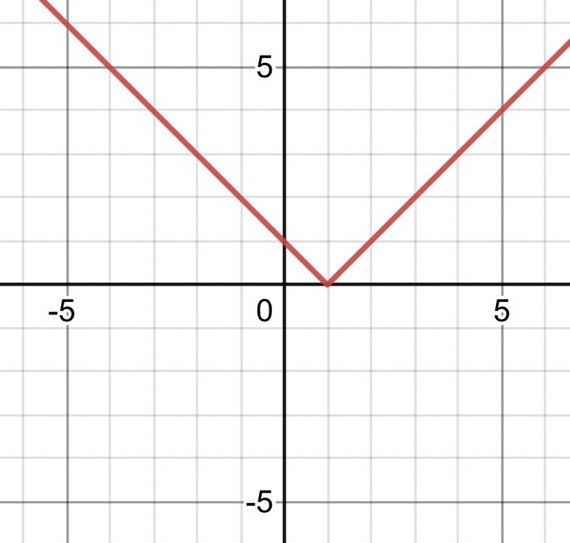
あれ？　対称的な形じゃない？

対称性の本質を思い出してほしい。

$ y=|x-1| $ において、 $ X=x-1 $ とおいてみると、 $$ y=|X| $$ この $ X $ についての方程式で、 $ X $ を $ -X $ に置き換えると $$ |-X|=|X| $$ となり、元の方程式 $ y=|X| $ に一致する。

$ X $ を $ -X $ に置き換えても成り立つということは、グラフが直線 $\boldsymbol{X=0} $を軸に対称であることを意味する。

$ X=x-1 $ であったから、直線 $ X=0 $ というのは $\boldsymbol{xy}$ 平面上の直線 $\boldsymbol{x=1} $ のことである。

グラフを見ると確かに $ x=1 $ を軸に対象になっている。

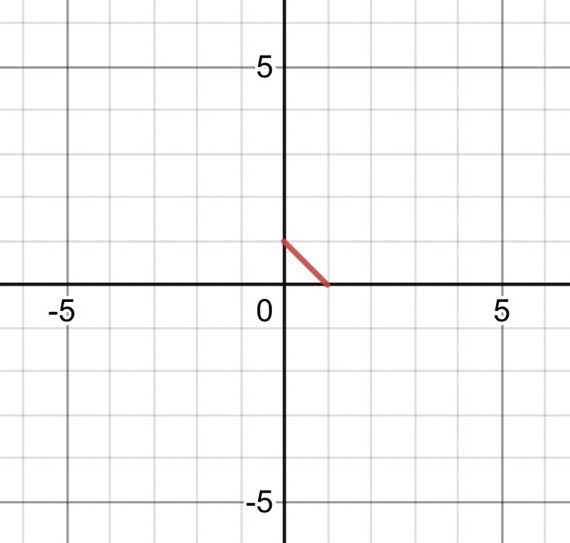
例

例3

$ |x|+|y|=1 $
対称性より $ x,y \geqq 0 $ とすると $$ x+y=1 $$

対称性を戻して

例4

$ |x-2|+|y-1|=1 $ のグラフを求める。
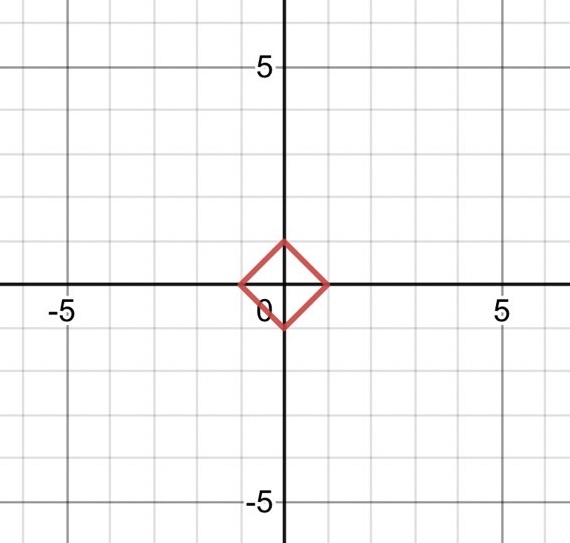
$ X=x-2,\quad Y=y-1 $ とおくと、方程式は $$ |X|+|Y|=1 $$ 対称性より、このグラフは直線 $ X=0, \quad Y=0 $ を軸に対称。
直線 $ X=0 $ は $ x=2 $、 $ Y=0 $ は $ y=1 $。
まず、対称の軸をかく。

$ X,Y \geqq 0 $ のとき $ X+Y=1 $。

対称性を戻して

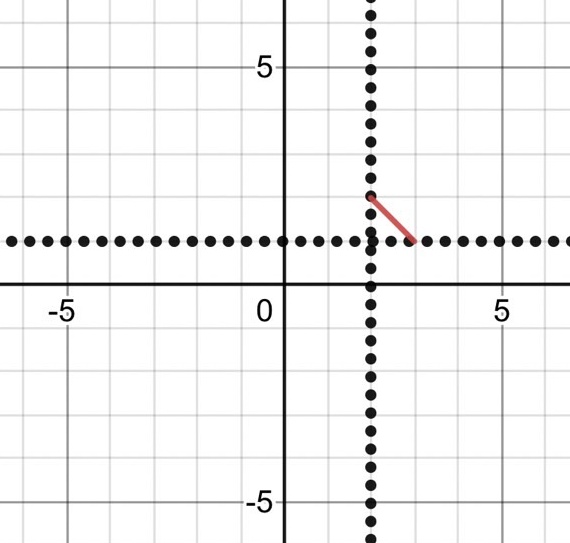
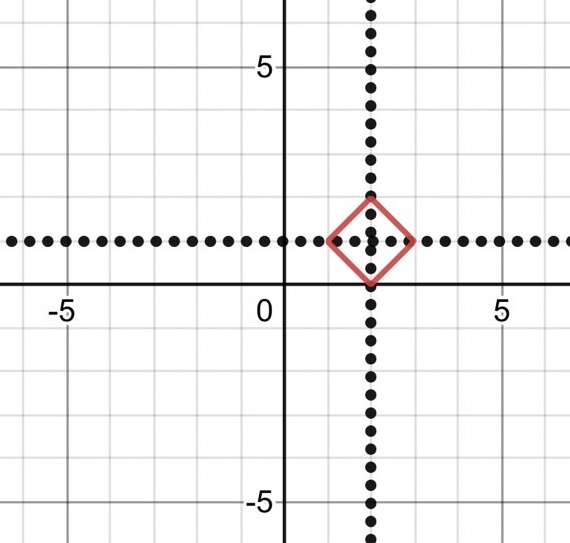
応用1 ──2文字の式の絶対値──

例5

$ |x+y|+|x-y|=1 $ のグラフを求める。 $$ X=x+y,\quad Y=x-y $$ とおくと
$ |X|+|Y|=1 $ より、直線 $ X=0, Y=0 $ を軸として対称。
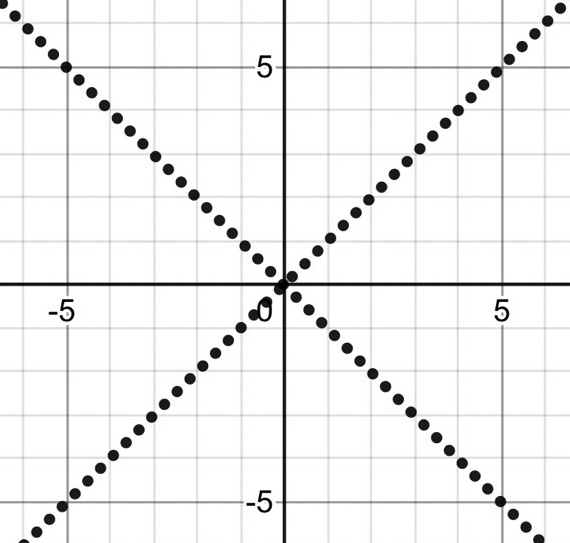
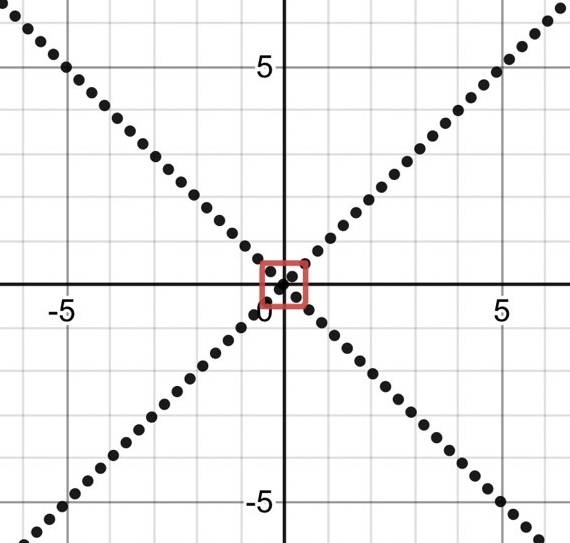
$ X=0 $ は $ x+y=0 $ すなわち $ y=-x $
$ Y=0 $ は $ x-y=0 $ すなわち $ y=x $
対称の軸をかく

$ X,Y \geqq 0 $ すなわち $$ y\geqq -x, \quad y \leqq x $$ のとき
$ X+Y = 1 $ より $ (x+y)+(x-y)=1 $、 すなわち $$ x=\dfrac{1}{2} $$

対称性を戻して

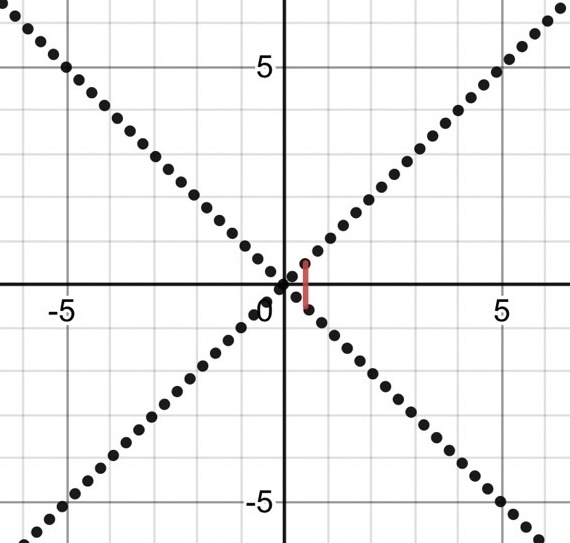
応用2

例6

$ |x+y-2|+2|x-y|=2 $ のグラフ。
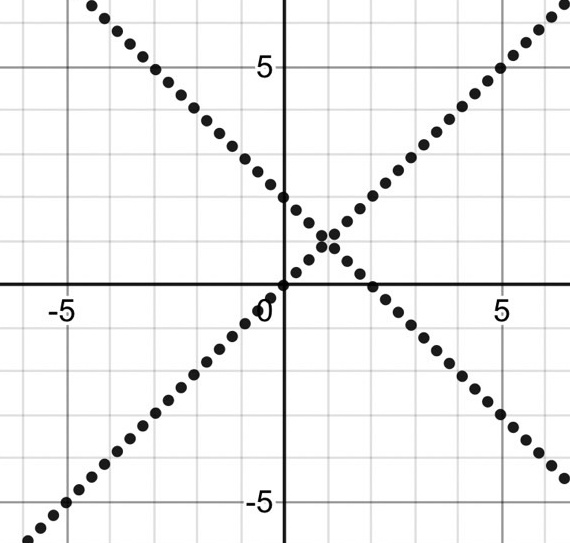
$$ X=x+y-2, Y=x-y $$ とすると
$$ |X|+2|Y|=2 $$ より、直線 $ X=0, Y=0 $ を軸として対称。
直線$ X=0 $ は $ y=-x+2 $ 、 $ Y=0 $ は $ y=x $。
まず対称の軸をかく。

$ X,Y \geqq 0 $ すなわち $$ y\geqq -x+2, \quad y \leqq x $$ のとき、 \begin{align} 2 &= X+2Y\\ &= (x+y-2) + 2(x-y)\\ &= 3x-y-2\\ y &= 3x-4 \end{align}

対称性を戻して

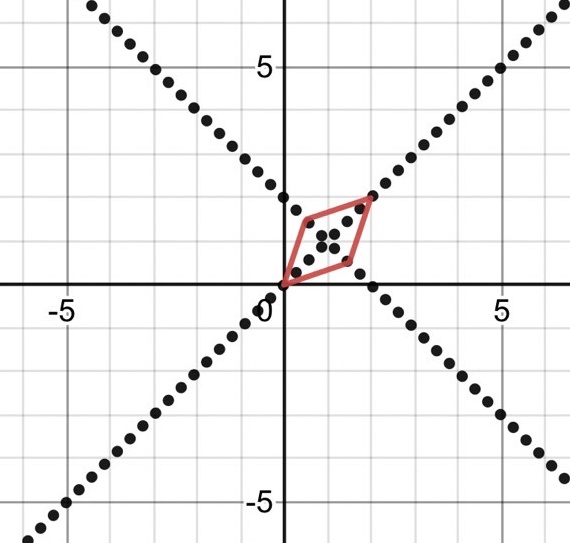
裏技的なもの

とりあえず手描きのを貼っときます。余裕があれば打ち込む。

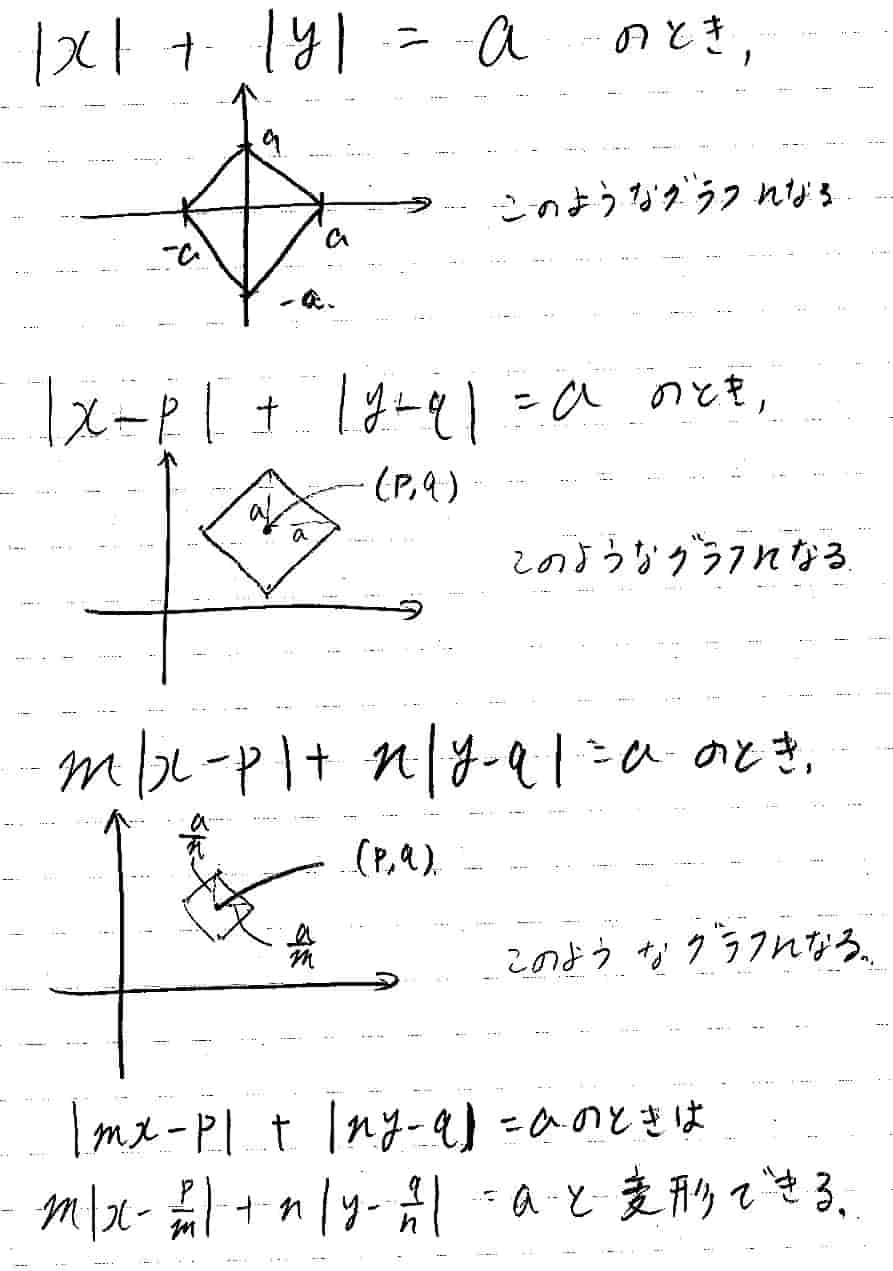
終わりに

冒頭でも述べたように、短い試験時間の中で4通りや16通りもの場合分けをしている余裕はない。対称性を使ってできる限り楽に解こう。

質問・感想